(A) This is the definition of an adiabatic process.
(B) 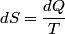 Because the process is adiabatic, 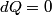 , so , so 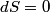 , so the integral of , so the integral of 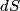 over the entire process also equals 0. over the entire process also equals 0.(C) By the Second Law of Thermodynamics, 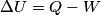 where 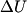 is the change in the internal energy of the gas, is the change in the internal energy of the gas, 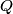 is the heat added to the gas, and is the heat added to the gas, and 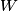 is the work done BY the gas. Since the process is adiabatic, is the work done BY the gas. Since the process is adiabatic, 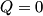 and and 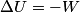 . . 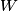 is given by is given by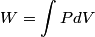 Therefore, 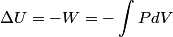 (D) As discussed in part (C), 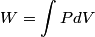 (E) The temperature of an ideal gas is related to the internal energy by 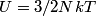 where 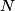 is the number of gas molecules, is the number of gas molecules, 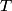 is the temperature of the gas, and is the temperature of the gas, and 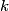 is Boltzmann's constant. The internal energy of the gas is not constant (see part (C)), so the temperature cannot stay constant. is Boltzmann's constant. The internal energy of the gas is not constant (see part (C)), so the temperature cannot stay constant.Therefore, answer (E) is correct. |